Casting Errors
To begin with, there is no way that it is possible to cast or otherwise manufacture a set of balls which are of exactly the same weight. In any process, there are always a number of variables, such as casting temperature, mold compression, tiny particles or voids in the mold or in the metal, local variations in alloy purity, etc, which each have their own separate effect on the final weight of the cast ball. Some tend to add weight and some decrease it, but the sum of a set of random variations such as these will create what, in statistical terms, is called a "Normal" distribution. If you were to weigh each ball and plot its weight, you should see the "Normal", bell-shaped curve, where most weights fall within plus or minus a certain amount from the mean, or average, weight. This type of weight variation is very hard to reduce beyond a certain point, since there are too many variables to control. However, there are also certain types of variables, called "monotonic", which always act in one direction and can throw off the smooth bell-shaped curve. An example of this is would be voids in the casting. A statistical analysis can largely separate out these types of errors and tell us how much variation we can expect if everything else goes well. The statistics of a "Normal" distribution tell us that 67% of the objects will fall within +\- one "Standard Deviation" (SD) of the mean, and 93% will fall within +\- two SDs. This, of course, assumes a "Normal" distribution, which we should get if all variables are well-controlled and completely random. Variations from "Normal" can be calculated, and items that do not fit this model can be eliminated.
How the Experiment Was Done
I used a dual-cavity Lee 0.433 inch ball mold and a Lee 5 lb. Production Pot which pours from the bottom. The lead was from scrap plumbing pipes, with any solder removed, and it was easily scratched with my fingernail and thus presumably close to pure. After the initial melting, fluxing and skimming, I set the pot temperature control to "6" and then gently and slowly heated the bottom of the closed mold with a propane torch until saliva on my finger "popped" when placed on the top of the mold. My casting technique was to hold the mold on the spout at a sligth angle and open the value for about five seconds, then I simultaneously dropped the mold and closed the spout, resulting in a small puddle of lead on top of each sprue hole, which took about five seconds to solidify; this prevented any surface air voids from forming as the lead solidifys and shrinks in the sprue hole. I cast half a dozen discards, then cast continuously until I had two piles of 90 balls, one from each half of the mold. The balls were weighed to the nearest 0.1 grain on a Lyman LE-500 electronic scale, and the weights were entered into a statistical analysis program,
The two graphs below show the distribution of ball weights from both the inner and the outer mold cavity.
The height of the bars represent the number of balls in each 0.1 grain weight group. The fact that some groups
are empty makes the curve appear uneven but is a perfectly normal occurrence in a random sample such as
this.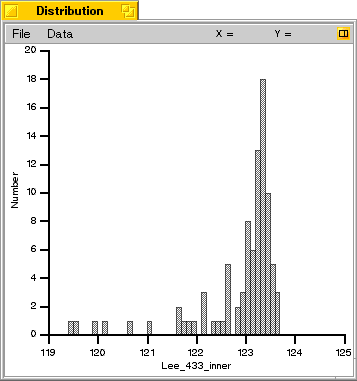
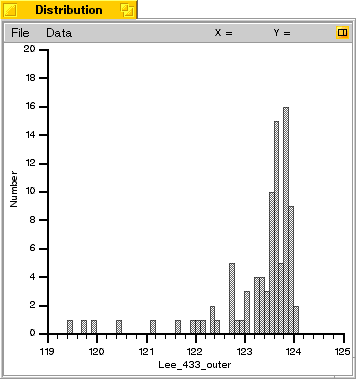
As you can see from the graphs, the weights cluster to the heavier end, with a number of lighter outliers trailing off. This indicates that there is a factor which is substantially decreasing the ball weights in some cases. There is also a small overall difference in the ball weights from each mold cavity.
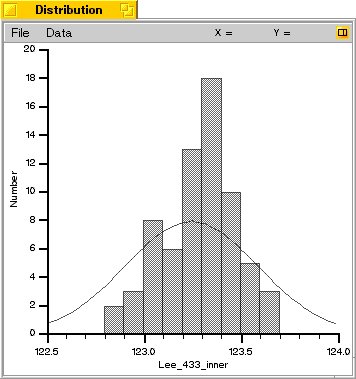
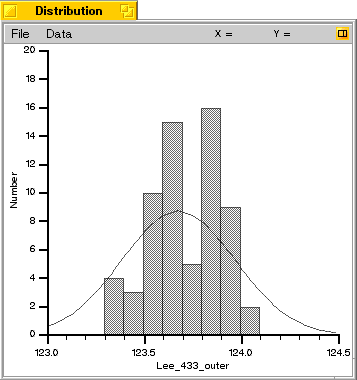
These two graphs above show the results after removing the balls in the outlying tail of the distribution and recalculating the results. Note that the weights have a more characteristic bell-shaped distribution, which is expected. The smooth curve shown on the graphs represents a perfect "Normal" distribution. An examination of the lighter balls which were excluded showed that all of them had small internal voids, similar to those shown on page 55 in the May issue of Muzzleblasts. As with those in the article, the voids were present even though there was no visible pit on the sprue.
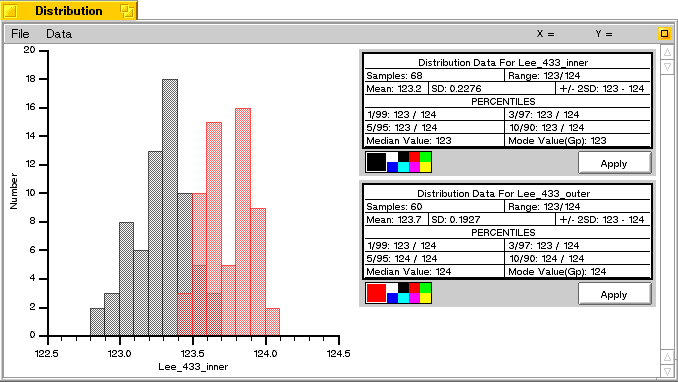 This graph shows the weight distributions from both cavities, with the balls from the outer
cavity shown in red and those from the inner cavity shown in black. As you can see, the mean weights are 0.5
grains different; the standard deviation of each cavity is about 0.2 grains, so this creates a small region of
overlap. The average ball diameter from the heaver cavity was about 0.0005" larger, which accounts for
the average weight differences.
This graph shows the weight distributions from both cavities, with the balls from the outer
cavity shown in red and those from the inner cavity shown in black. As you can see, the mean weights are 0.5
grains different; the standard deviation of each cavity is about 0.2 grains, so this creates a small region of
overlap. The average ball diameter from the heaver cavity was about 0.0005" larger, which accounts for
the average weight differences.
So - What Does It Mean?
From the original 90 balls from each cavity, about 60 were within the envelope of expected "Normal" distribution and about 30 were not. It is assumed that those within this distribution range were unaffected by the voids or related problems. To try and confirm this, several "Normal" balls were sliced, and no voids were seen.
However, now we have a pile of about 120 balls with a little over one grain variation in weight, which is certainly more than the "no more than a tenth grain variation" preached by some shooters. If we used that rule, we would get about two dozen balls, which is a very poor yield for the work. Since there is no way that I could determine if this one grain spread caused a looser group than a lesser variation (unless I mounted a 20X scope on my flinter), I turned to a ballistic simulator to see if the differences could be calculated.
A ballistic simulation was set up for two balls of .433" diameter, one weighing 123 grains and the other 124 grains. A muzzle velocity of 1400 fps was given, with a sighting point of 50 yards, with a 10 mph crosswind. The results showed that at 100 yards, there was a two fps difference in velocity but no discernable difference in drop or crosswind drift. At 200 yards, there was a 0.5" greater drop in the lighter ball and 0.3" more crosswind drift. My conclusion from this is that no human shooter could ever see the difference. However, if the weight differences were due to an internal void, the results might be different. A one millimeter void will give about a one grain weight drop, and if this void were off the center axis of the ball, some wobble would be expected and might have a greater effect on accuracy than evenly distributed weight differences due to tiny variations in ball diameter.
In summary, I believe that balls culled from the center of the "Normal" region should shoot as well as any, and that mixing two different ball "populations" (such as from different cavities) should have no deleterious effect on normal shooting. In the experiment shown here, this gave a weight spread of about one grain.
