'The itsy-bitsy granule went down the powder spout...'
First, an important clarification: I am using the familiar English system of grain weights for powder quantity because there is no such thing as a 'grain volume', so any reference to 'grains' means only the weight. To prevent any confusion, I will refer to the individual powder grains as granules.
So just how 'bitsy' are the granules?
The granules vary a LOT in size. I tried directly measuring them, both with a micrometer and with optical image measuring methods, but neither result seemed very useful considering the range of sizes. I then decided to calculate the average grain size as if each granule was a little sphere. We know this isn't true, but treating them this way might 'wash out' the variations and give a useful result, at least in terms of average burn time per granule.
To calculate
this size, 'all' that was needed is the number of granules per grain of powder and the density of the
powder granules (not the bulk density). I counted out about 500 granules of powder for each powder type and
granulation and weighed them on a laboratory balance; this gave me the average grain weight. The density
(weight/volume) was a little harder, since I needed the density of just the granules, not the air between them
that one would also measure if you just saw how much volume the bulk powder filled. Our old friend Archimedes came to the rescue to help with the calculation. About 100
grains of powder was carefully weighed, and this was slowly added to a glass tube (shown on the left)
containing 100% isopropanol, and the volume of the isopropanol displaced by the weight of the powder allowed
the density to be calculated. Pure isopropanol was used because it easily wets the granules, driving out the
entrapped air, and because it will not dissolve or interact with any components of the powder.
In counting out the powder granules under a microscope, I was struck by how much variation there was in a given granulation and how varied the shapes were. Black powder (and Shockey's) is made by pressing the powder into a cake and then fracturing the cake and sorting the granules with screens. Since some of the fragments can be two or three times as long as wide, whether they fall through the screens can depend upon their orientation as well as their volume. I suspect this is why fractured powders (whether or not they are polished later) have at least a three-fold range of sizes - and therefore a nine times volume difference among their granules. The greatest size difference was with Shockey's, which had very irregular and 'flaky' grains with a size variation at least twice that of black powder. The other black powder substitutes were surprisingly uniform, looking like they were made by a completely different process, probably wet granulation; in particular, the Goex Clear Shot 2F granules were almost perfectly spherical and very uniform in size.
The results are shown below, where the 'Grains/cu.in.' is the bulk density, as in a powder measure, 'Packing' is the relative amount of powder to air in a volumetric measure, 'Granules/grain' is the average number of powder granules in a grain weight of powder, 'Gran.S.G.' is the specific gravity of the powder granules (water has a S.G. of 1.0), 'Granule Dia.' is the calculated granule diameter in inches, as if the granules were actually little spheres.
| Powder | Swiss 3f | Swiss 2F | Elephant 3F | Goex 2F | 777 3F | Shockey's 3F | Clear Shot 2F | Clear Shot 3F |
|---|---|---|---|---|---|---|---|---|
| Grains/cu.in. | 262 | 272 | 256 | 239 | 198 | 204 | 235 | 234 |
| Packing | 54.1% | 57.4% | 51.0% | 49.8% | 44.9% | 39.9% | 51.6% | 51.5% |
| Granules/grain | 266 | 96 | 217 | 55 | 452 | 116 | 61 | 289 |
| Gran.S.G. | 1.92 | 1.88 | 1.99 | 1.90 | 1.80 | 1.97 | 1.80 | 1.80 |
| Granule dia. | 0.030 | 0.042 | 0.032 | .052 | 0.027 | 0.040 | 0.051 | 0.030 |
Deflagration - What the powder grain does
For our purposes here, deflagration is the rate at which a flame front moves through a solid mass of propellant. Deflagration is literally a burning due to a transfer of heat in the material, which separates it from detonation, which is a chemical decomposition caused by the passage of a pressure wave through an explosive. The problem is, how does one measure how fast an individual powder grain burns, and how does this burn rate vary under different conditions (for example, in a muzzle loader charge versus in open air). There is surprisingly little quantitative information on this; I recall reading a report [I can't find the reference, but if I do, I will add it] that some powder makers would load their powder into a lead tube and then roll it to a flat strip containing a thin layer of powder. One end of the strip was lit, and the progression of the flame to the end of the strip was timed. There was only a single reference to the actual speed, which was around 2 1/4 inches/second, and although this may have been a useful measurement, I doubted how well this relates to the actual burning speed of an individual powder grain, so I designed some experiments to attempt to find out.
To start, I wanted
to find out how fast an isolated granule would burn, but even for a given granulation size, black powder
granules vary a lot, and small granules will burn up faster than larger ones. To get around this problem, I
made powder 'granules' of exact dimensions and also large enough that the burn time could be
accurately measured. A small quantity of the candidate powder was reduced in a mortar and pestle so that the
surface skin of the granules was fragmented. The powder was then pelletized by pressing it in the die shown
here at about 10,000 PSI to form a solid mass 0.125" diameter X roughly 0.10" long.
The pellets were epoxied to a sheet of foil which was then taped to a support so they wouldn't fly away after ignition. The top of the pellet was ignited by touching it with the tip of a hot wire, and the burn was recorded by a Samsung TL-350 camera shooting at 240 frames/second. If you click on the image of the burning pellet, you will be taken to a video of the test series; the numbers in the video are the actual pellet thicknesses and the camera frame rate. The frames from the start of burning to the end were counted to get a burn speed for the powder. Note that the deflagration rate is a function of the powder composition and is not affected by granulation size, although the individual granule burn time is. All measurements were performed in triplicate (the agreement of values was very good), and the results are shown below in inches/second for several powders:
| Powder | Goex BP | Swiss BP | Elephant BP | 777 | Shockey's | Clear Shot |
|---|---|---|---|---|---|---|
| Burn Speed | 0.47 | 0.35 | 0.37 | 0.17 | 0.14 | 0.45 |
I found these results to be very surprising, since I had always heard (and believed) that Swiss powder was the fastest burning, but in this case, Goex burned 34% faster, while Elephant and Swiss were essentially the same. The two other surprises were how fast Clear Shot burned and how slowly (and strangely) Shockley's Gold burned, although the deflagration rate alone is not the sole arbiter of the power of a propellant. As some confirmatory evidence, in a 1989 article from Rhodes University in South Africa, the burning rates in packed powder columns were measured at 0.37 inches/second, closely matching my results.
But what about 'real' granules?
Just to make sure that my pelletizing of the powder didn't affect the basic deflagration
rate, I recorded the burn times of a few larger powder granules to see if the values were reasonably close to
what I got before. I tried to find relatively large and flat granules, which were ignited by a high-frequency
electric discharge delivered to the top of the grain by a sharpened wire. If you click on the image, you will
be taken to a video of the single-grain burns. The results from the single-grain burn tests showed a
deflagration rate somewhat higher than what was calculated from the pellet tests, but this was not unexpected
since, even though the grain was lit from a single point, the combustion front rapidly crept around the grain
and tended to burn it from both sides, making it burn faster. However, in both cases, there seems to be a
severe problem - if powder burns this slowly, all we have is a pea-shooter! Here is what I mean. If we have a
muzzle loading rifle with a barrel 36" long and we are shooting a ball with a muzzle velocity of 1400
fps, we can calculate about how long the ball takes to accelerate down the barrel and exit the muzzle. In this
case, if we assume an 'average' velocity of 700 fps down the barrel (starts at zero in the breech and
reaches 1400 at the muzzle), the bullet takes about 4.5 milliseconds to exit, but if our powder grains seem to
take 50 milliseconds to burn (even if they were all ignited at the same time - which they aren't), we are
certainly not getting a lot out of the powder. Therefore, we have to assume that something else is going on to
speed up the powder's burning time.
But I degress...
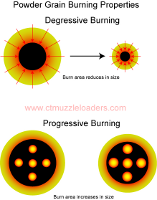There is a
somewhat confusing set of definitions regarding how powder burns. Modern smokeless powders are described as
'progressive' burning, which can actually have two separate meanings. One meaning of progressive
burning has to do with the geometry of the powder granule, where the combustion area increases as the powder
burns, thus liberating increasingly more energy. In this case, the opposite of 'progressive' is not
regressive, conservative, or even Republican, but is 'degressive'. In a degressively burning powder
granule, such as black powder, the combustion area shrinks, with rapidly decreasing energy release as the
granule burns away. These are illustrated by the diagram on the left (click to enlarge).
There is, of course, yet another definition of 'progressive burning', which is that the rate of deflagration increases with increasing chamber pressure. Smokeless powder is quite 'progressive' in this sense, so one can have grains which are degressive in geometry and progressive with pressure. As you can begin to see, all these factors need to be delicately balanced for smokeless powder, where a relatively small increase in load or change in powder type can increase the pressure, which in turn markedly elevates its deflagration, which further increases the chamber pressure, etc, etc, etc... On the other hand, the deflagration rate of black powder is much less sensitive to pressure, but as we saw with the deflagration rate measurements, black powder must have some pressure-progressive properties, otherwise it just wouldn't be effective if it burned at the same speed in a gun barrel as it does in open air. To understand what is happening, we need to take a closer look at the inside of the powder granule
Black Powder, Inc. - Why 'incorporation' matters
Incorporation of black powder is the process whereby the constituents are reduced in size to form an intimate mixture. To see why this matters so much in its performance, think of it this way: If you were to just throw the powder ingredients into a pot and then toss in a match, it is unlikely much would happen. If you then stirred the crystals and chunks around a bit, you might get it to burn, but it would not be a useful propellant. Taking it another step, if the ingredients were ground together for a bit so the components were in better contact, it would definitely burn. As the grinding and mixing (the incorporation) progressed and the individual grains became increasingly fine, the burning speed would increase, although each additional incorporation would not produce as much improvement as the last one - a case of diminishing returns. As a final step, if the mixture was compressed to the point where the sulfur plasticized and flowed around the other ingredients, the components would be as completely combined as possible.
Why this matters so much is because the reaction (deflagration) of black powder can only take place, in effect, where the grains meet and allow mixing of the oxidizer and fuel. With smokeless powders, each molecule contains its energy locked within itself and only needs a molecular bond to be broken to be released. Therefore, the deflagration 'reaction' does not have to travel as far in smokeless powder as it does in black powder.
For the reaction to start in black powder, the temperature must be raised enough for oxygen to be released from the potassium nitrate and combine with the fuel ingredients (the charcoal and sulfur). Surprisingly, there seems to be some disagreement about the ignition temperature of black powder; the official Material Safety Data Sheet (MSDS) for black powder lists it as 464°C (867°F), which I believe is clearly too high. Other figures hover at or a little over 300°C (572°F), which sounds more like it. The discrepancies may be due to how the temperature is applied or how well incorporated the powder is. Pure sulfur will ignite at 216°C, but it may need a higher temperature if it closely incorporated into a mixture, and potassium nitrate decomposes at 400°C, which is likely to be a ceiling value for mixtures containing it.
Black powder - A true progressive after all
For deflagration to continue in a powder granule, the burning surface must communicate heat to the underlying layers and raise their temperature to the ignition point, continuing the burning process until the granule is consumed. In a solid granule, heat can be transferred by two processes, conduction and radiation. Conduction is the direct transfer of heat through actual contact (like picking up a hot object), while radiation is the transfer of heat across a transparent medium (like the warm feeling coming from sitting near a campfire). Because a black powder granule is not at all transparent, we are left with conduction (although in smokeless powder there can be some heat transfer through radiation). Since a black powder granule is relatively incompressible, pressure will have no effect on internal heat transfer, but it will have an effect on how well heat is conducted from the gaseous burning surface to the underlying solid. As the pressure rises, the conductivity of the flame itself is increased, allowing much faster heat transfer to the underlying layers, just like being able to gently pick up a piece of hot metal that would burn you if you grabbed it hard. As this conductivity increase will only affect the boundary layer and not any underlying powder, the effect would not be directly proportional to the pressure increase, but some fraction of it. For example, if the deflagration rate were to increase by 10% in proportion to the pressure increase, at a breech pressure of 3000 PSI, 200 times the normal atmospheric pressure at which the deflagration data was taken, the grain burning times would change as follows, with the burn times expressed in milliseconds:
| Powder | Granule Dia | Air Deflag.Rate | Air Burn Time | Pressure Burn Time |
|---|---|---|---|---|
| Swiss 2F | 0.042 | 0.35 | 60 | 2.9 |
| Swiss 3F | 0.030 | 0.35 | 43 | 2.1 |
This kicks the grain consumption rate into a range that makes the powder actually do something, but how do we find the 'magic multiplier' factor? At this point, I can't think of a simple (and safe) experiment to measure it directly, but my upcoming computer model may let me make a good guess based on the model's performance compared to real world data. It would be much more satisfying (to me) to be able to measure the rate directly under controlled conditions, but for now, this will have to do.
But everything has a limit...
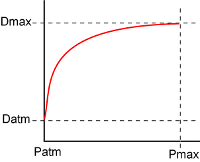With a progressive-burning
powder, the pressure increases the burning rate, which increases the pressure, which - etc,etc... This type of
situation is known as a positive feedback loop, and the consequences are that whatever the
initial conditions were, the results are quickly driven to the limit. In the case of black powder, what
exactly are the limits? For example, pressure starts at roughly atmospheric pressure (Patm, 14.7 psi) but
cannot increase to infinity, so there must be an upper limit to the pressure which can be generated by black
powder. Fortunately, this figure can easily be determined from the amount of gas evolved and the temperature
rise due to the deflagration. From the packing data above, we can see that a charge of powder is about half
air, so this also limits the possible maximum pressure. Based on my calculations and references from the
literature, for granular black powder the Pmax is about 37,000 psi. The second limit is the maximum
deflagration rate at maximum pressure. Although the transfer of heat within the deflagrating layer will go up
continuously with pressure, the pressure has no effect on heat transfer in the solid underlying powder.
How fast heat can be conducted in the grain itself then becomes the limiting factor for deflagration (Dmax).
Therefore, we have a situation where the powder grain deflagration progresses from that at atmospheric
pressure (Datm at Patm), to that at the maximum possible pressure (Dmax at Pmax). The graph to the left
illustrates this asymptotic
relationship, which illustrates the point of diminishing returns for powder burning speed as the pressure
increases. However, from my practical standpoint in creating an internal ballistic simulation, I still
don't know what Dmax actually is. In the last analysis, I will still have to make an educated guess based
on how well the simulator muzzle velocity matches real-world results.
Ignition propagation - The other 'burn'
When the powder charge is ignited, all the granules don't all immediately ignite, especially in a flintlock. The ignition has to propagate through the charge by leaping from one grain to another. A 1952 study by Blackwood and Bowden showed that adjacent grains were ignited by a hot spray of liquid potassium salts ejected from burning grains, and this propagation speed varied from about 190 m/sec (623 fps) to as much as 400 m/sec (1312 fps) in a fully-confined powder explosion. Another recent Russian paper confirms this in a separate set of experiments on black powder explosions in open tubes. It is likely the lower figure of 190 m/sec is the speed reached in a firearm, which means a 1" long powder charge could completely ignite in as little as 0.13 milliseconds.
Conclusion
What started out to be a seemingly simple question turned into several weeks of work and experimentation, with the end result still leaving some unanswered questions. One thing clearly stood out - black powder, contrary to many popular assumptions, is indeed as progressive-burning as smokeless powder, although smokeless has a much higher energy content and can create higher and more sustained pressures. The other 'burning', charge ignition, seems to happen much faster than I originally supposed, which helps explain to me why flintlocks get virtually the same muzzle velocity as percussion arms, regardless of the less efficient ignition system.
